5 Petri Net
A Petri net is a bipartite directed graph composed of places and transitions, connected by arcs, that can be weighted, where the weight represents the number of tokens destroyed and created.
Places represent buffers, channels, conditions or state. Input places can serve as input data, required resource, a condition or preconditions. The output places can serve as post conditions, output data, resources released, a conclusion, or a buffer.
Transitions represent events or transformations.
The state of a Petri net is called marking, and it’s determined by the distribution of tokens over the place.
A transition is enabled if each of its input places contains tokens. When a transition fires, it consumes a token from each input place and creates a token in each output place. Firing is atomic in the sense that all of the consumption and creation of tokens takes place at one time.
5.1 Mathematical definition
A Petri Net N is a tuple N = (P, T, I, O, M_0), where
P is the set of all places
T is the set of all transitions
I: P x T \rightarrow ({0, 1, 2, …}) is the pre-incidence function representing input arcs (preset)
O: T x P \rightarrow ({0, 1, 2, …}) is the post-incidence function representing output arcs (postset)
M_0: P \rightarrow N is the initial marking representing the initial distribution of tokens.
P \cap T = \varnothing
An alternative way to represent the transition functions is to suppress the place as an argument and using place in the output of the functions to correlate place and count of directed arcs into or out of the place. So instead of defining I(p_i, t_i) and O(t_i, p_i) we define I(t_i) = (I(t_i, p_i) \forall p_i \in P), same for O(t_i).
Let E(M_i) be the set of all transitions enabled at M: M_i \geq I(t) \iff t \in E(M_i)and the firing of t takes the net from M_i to M_j with the following resulting marking: M_j = M_i - I(t) + O(t)
5.2 Petri Net structures
Sequential execution
Concurrent execution
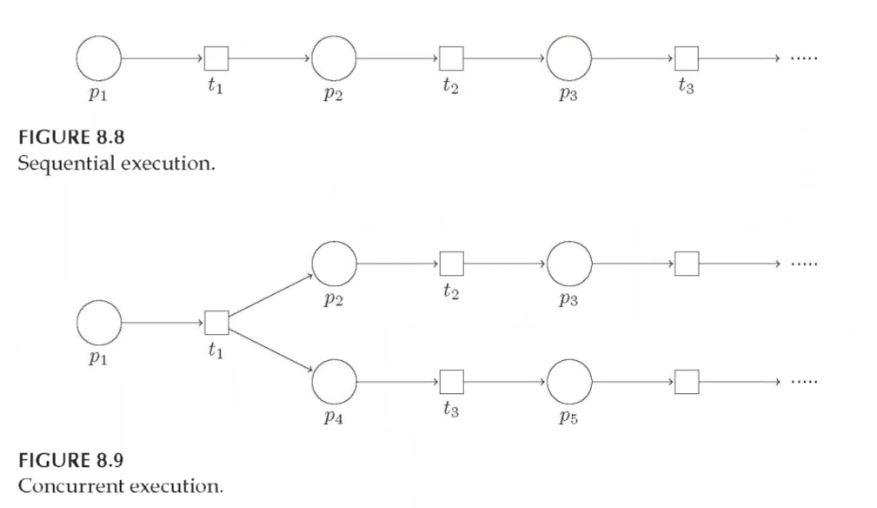
Synchronization: taking independent sequences and forcing them to reach specific states before continuing on with execution
Nondeterminism: can be solved in a non-deterministic way or in a probabilistic way, that is, assigning probabilities to he conflicting transitions.
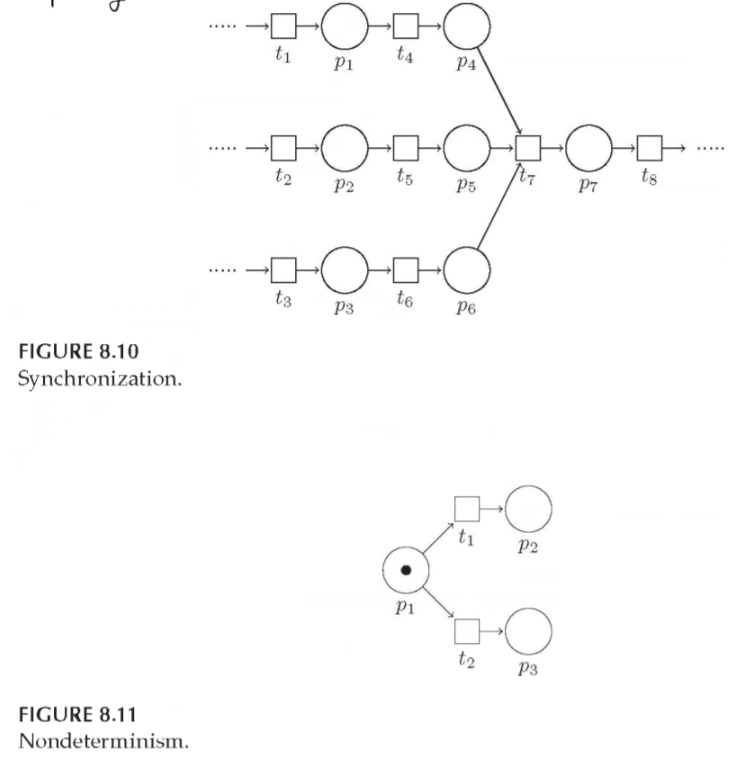
Loop
Source: transition that has no input place but does have an output place, so it is enabled at all times.
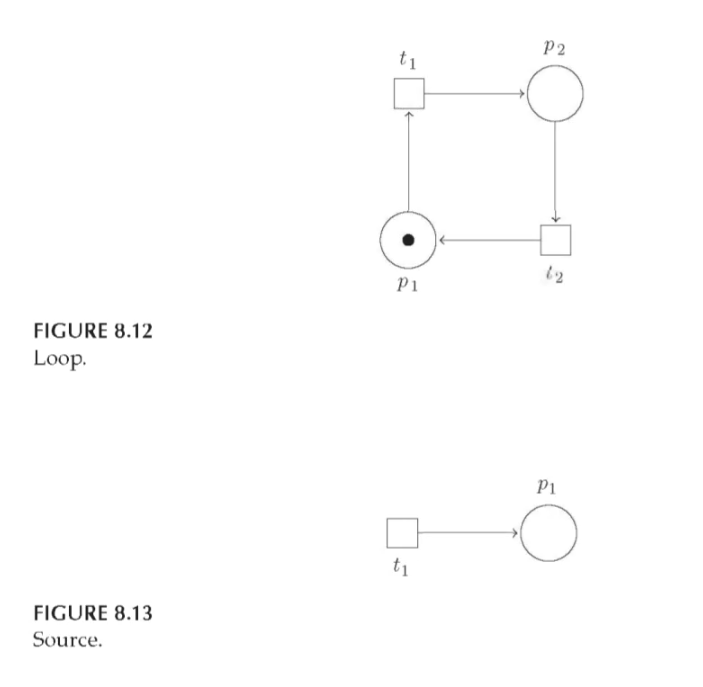
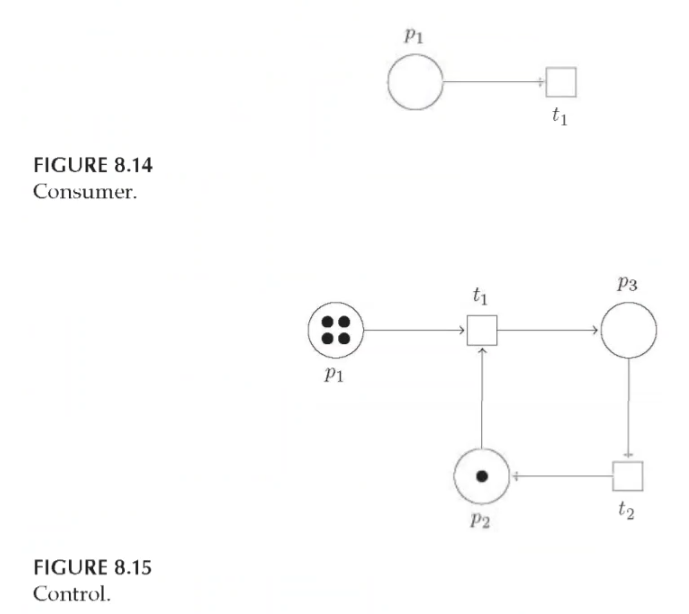
Consumer: the opposite of a source: is a transition that has an input place with no output places
Control: can be incorporated as limiter, or as a break point for the loop
- Accumulator: the opposite of a control. Rather than a place that holds tokens which are to be consumed, an accumulator is a place where tokens are created and never consumed
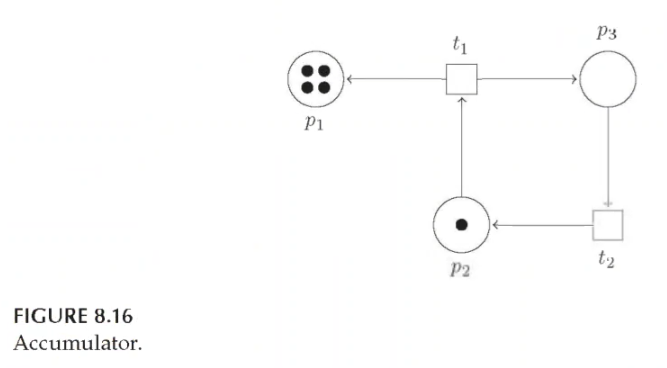
- Safe mutual exclusion
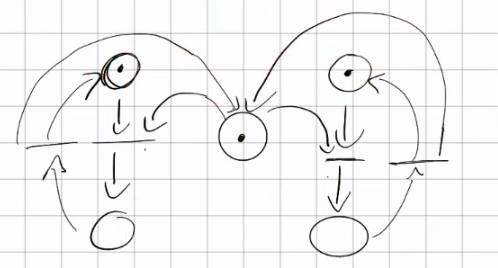
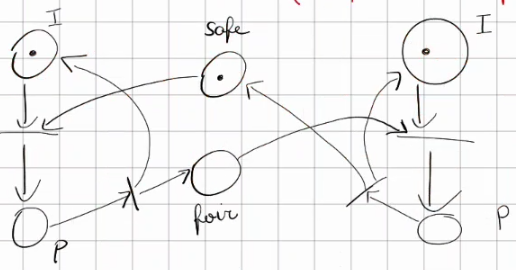
- Safe and fair mutual exclusion
5.3 Petri Net Behavior
A Marking M_n is reachable from M_0 if there exists a sequence of firings that transform M_0 in M_n. The set of all markings reachable from marking M is denoted by R(M).
5.3.1 Reachability Tree
Given a Petri Net and an initial marking it is desirable to know all of the states that can be reached by firing transitions. This is done using the reachability tree, constructed by the following algorithm:
Label the initial marking M_0 as the root and tag it “new”
\forall M new:
If \exists M_i appeared before in the tree such that M = M_i, then tag M “old” and go to another new marking
If E(M) = \varnothing, tag M “dead end” and go to another new marking. If you encounter one of this marking then the net is not deadlock-free
While there exists enabled transitions at M, do the following for each of them:
Obtain the marking M^{'} that results from firing t at M
Introduce M^{'} as a node, draw an arc with label t from M to M^{'}, and tag M^{'} as “new”
Merging the same nodes in a reachability tree produces the reachability graph
5.3.2 Boundedness
A place p is k-bounded if the number of tokens in p is always less than or equal to k > 0 \forallM \in R(M_0).
A place is safe if it is 1-bounded.
If every place in a Petri Net is 1-bounded then the Petri Net is safe.
5.3.3 Liveness
5.3.3.1 Deadlock definition
Deadlock refers to a specific condition in which the processes of a group are each waiting for another process to perform some action. The result is that none of the processes in that group are able to perform an action.
A Petri net modeling a deadlock-free system must be live. A transition t is live if it can always be made enabled started from any reachable marking: \forall M \in R(M_0), \exists M^{'} \in R(M) \; \text{such that}\; M^{'}[t >
This implies that or any reachable marking M, it is possible to fire any transition in the net by progressing through some firing sequence. Given that this is too restrictive different levels of liveness are defined.
Denote by L(M_0) the set of all possible firing sequences starting from M_0. A transition t is
L0-live (dead): if there is no firing sequence in L(M_0) in which t can fire
L1-live (potentially fireable): if t can be fired at least once in some firing sequence in L(M_0)
L2-live: if t can be fired at least k times in some firing sequence in L(M_0) given any positive integer k
L3-live: if t can be fired infinitely often in some firing sequence in L(M_0)
L4-live (live): if t is L1-live in every marking in R(M_0)
A Petri net is live if all transitions are live. A marking M is a deadlock if no transition is enabled at M. A Petri net is deadlock-free if it does not contain any deadlock in any reachable marking from the initial marking.
5.3.4 Reversability
A Petri net is reversible if for each reachable marking M, M_0 is reachable from M:
\forall M_i \in R(M_0), M_0 \in R(M_i)
5.3.5 Fairness
Two transitions t_1 and t_2 are in bounded-fair relation if the minimum number of times that either one can fire while the other is not firing is bounded.
A Petri Net is a bounded-fair net if each pair of transitions are in a bounded-fair relation.
5.3.6 Incidence Matrix
Given n transitions and m places, the incidence matrix is defined as A \in R^{n \times m} and a_{ij} = O(t_i, p_j) - I(t_i, p_j)
5.3.7 T-Invariant
It is desirable to find a firing sequence transforming a marking M_0 back to M_0.
A T-invariant is an integer solution of A^T x = 0
The non-zero entries in a T-invariant represent the firing counts of the corresponding transitions, which belong to a firing sequence transforming a marking M_0 back to M_0.
5.3.8 S-Invariant
An S-invariant is an integer solution of Ax = 0
The non-zero entries represent weights associated with the corresponding places so that the weighted sum of tokens on these places i constant for all marking reachable from an initial marking.
These places are said to be covered by an S-invariant.
The goal is to identify minimal subsets, that is, subsets that are S-invariant and are not unions of other S-invariant subsets
5.4 Timed Petri Net
Petri nets that contain timing variables are called timed Petri Nets. The firing rules are defined based on the timing variables. We only discuss timed Petri nets in which timing variables are assigned to transitions.
5.4.1 Deterministic Timed Petri Net
A deterministic timed Petri net (DTPN) is a 6-tuple (P, T, I, O, M_0, ST), where (P, T, I, O, M_0) ius a regular Petri net, and ST: T \rightarrow R^{+} is a function that associates each transition with a deterministic firing time, called the static firing time of the transition. ST(t_i) is the delay of the transition t_i from being enabled to firing.
In addition to static firing time, there is also a dynamic firing time for each transition in DTPN. We always assume a timed Petri net starts running at time 0 from the initial marking.
We call a transition’s remaining static firing time in a marking the dynamic firing time, denoted by DT.
In a DTPN, the marking only determines if a transition can fire; all enabled transitions’ dynamic firing times together decide which transition to fire next. We define a marking together with the dynamic firing times of all enabled transitions in the marking as a state of a DTPN. A state corresponding to M_i is denoted by: S_t = (M_i, DT_i)
The transition t_k is enabled in M_i, that is: M_i \geq I(t_k)
The next marking after a transition fires in M_i is M_i^{'}.
Preconditions:
t_k can fire at the time τ in the marking Mi if and only if for any input place p of t_k, there have been the number of tokens greater than or equal to I(t_k, p) in p continuously for the time interval (τ - τ_k, τ), where \tau_k = ST(t_k).
t_k will fire at the time \tau if and only if:
DT_k(t_k) = min \{DT_l(t_l) | t_l \in E(M_i)\}where E(Mi) is the set of all enabled transitions in Mi.
Postconditions:
M_i^{'} = M_i + O(t_k) - I(t_k)
DT_l(t_l) = ST(t_l), for all t_l ∈ E(M_i^{'}) E(M_i)
DT_l(t_l) = DT_l(t_l) - DT_k(t_k), for all t_l ∈ E(M_i^{'}) ∩ E(M_i)
The first postcondition is the same as it is with regular Petri nets. The second postcondition states that for all newly enabled transitions in the new marking, their dynamic firing times are equal to their static firing times. The third postcondition states that for a transition that was enabled before the firing and continues to be enabled in the new marking, its dynamic firing time in the new state is the one in the old state minus the firing transition’s dynamic firing time in the previous state.
5.4.2 Performance Evaluation based on DTPNs
One application of DTPNs is the calculation of the cycle time of a class of systems in which job arrival times and job service times are known and fixed.
In a Petri net, a sequence of places and transitions p_1t_1 p_2t_2 ... p_{k-1}t_{k-1}p_k, is a directed path from p_1 to p_k if t_i is both an output transition of p_i and input transition of p_{i+1} for 1 \leq i \leq k-1.
If p_1 and p_k are the same place but all other nodes in the directed path are different, then the path is a directed circuit.
If in a Petri net every place has exactly one input transition and one output transition, then the Petri net is a decision-free Petri net and have two unique properties:
They are strongly connected: there is a directed path between any two nodes in such a Petri net.
The total number of tokens in a directed circuit remains the same after any firing sequence.
Let S(n_i) be the time at which a transition t_i initiates its n_i-th firing. Then the cycle time C_i of t_i is defined as C_i = \lim_{n_i \to \infty} \frac{S_i(n_i)}{n_i} It is proved that all transitions in a decision-free DTPN have the same cycle time C.
How to calculate C?
Consider a decision-free DTPN with q directed circuits.
For a circuit L_k, denote the sum of the firing times of all transitions in the circuit by T_k and the total number of tokens in all places of the circuit by N_k: T_k = \sum_{t_i \in L_k} ST(t_i) N_k = \sum_{p_i \in L_k} M(p_i) Both T_k and N_k are constants.
N_k can be counted at the initial marking. Obviously, the processing time required by circuit L_k per cycle, which is T_k, is less than or equal to the maximum processing power of the circuit per cycle time, which is denoted by CN_k. Therefore, we have T_k \leq CN_k \Rightarrow C \geq \frac{T_k}{N_k} The bottleneck circuit in the decision-free Petri net is the one that satisfies T_k = CN_k Therefore, the minimum cycle time C is given by C = \max\{\frac{T_k}{N_k} | k=1,2,...,q\} which corresponds to the best performance of the system modeled by the DTPN.